[SQL] MEDIAN 함수 없이 중앙값 구하기
by 소라고동_0. 들어가며
몇몇 DBMS 에서는 MEDIAN 이라는 함수를 제공하여 편리하게 중앙값을 구할 수 있지만, 제가 회사에서 작업하는 경우에는 이 함수를 지원하지 않아 직접 쿼리를 작성해야 했습니다.
그래서 포스팅에서는 SQL에서 중앙값을 구하는 방식에 대해서 간략하게 포스팅하려 합니다.
1. 중앙값에 대하여
우선 중앙값의 의미에 대해서 알아봅시다.
중앙값 (median)
: 통계 자료에서 변량을 크기 순서대로 늘어놓았을 때 그들의 한가운데 있는 값. 즉 전체 항을 이등분한 위치에 있는 값으로 통계 자료에서 대푯값의 하나이다.
(출처 : 네이버 국어사전)
위 설명에서 확인할 수 있듯 중앙값은 대표값을 구하려는 집단에서 모든 수를 나열했을 때, 정중앙에 위치한 값을 의미합니다.
그리고 중앙값의 장단점은 이렇습니다.
<장점>
이상치에 영향을 많이 받는 평균값과 달리 이상치에 영향을 크게 받지 않는다.
→ 이상치가 존재하거나 극단값이 존재할 때 사용
<단점>
값이 많이질수록 모든 값을 활용하지 못한다.( = 대표성이 옅어진다)
그럼 이러한 장단점을 가지는 중앙값을 SQL에서 구해보도록 하겠습니다.
2. SQL에서 중앙값 구하기
중앙값을 구하는 기본적인 아이디어는 단순합니다.
중앙값을 구하고 싶은 값들을 순서대로 나열한 뒤 정중앙에 존재하는 값을 뽑아낸다.
위 아이디어에서 핵심은 1.순서대로 나열, 2.정중앙의 값을 추출 인데요.
이 과정들을 윈도우 함수(Window Function) 중 row_number()를 활용하여 구현할 수 있습니다.
그리고 중앙값을 구할 땐 레코드의 개수가 짝수인지 홀수인지에 따라 방법이 약간 달라지는데요.
이 부분을 고려해야하기 때문에 약간의 아이디어가 필요합니다.
우선 레코드 수의 홀짝 여부에 따라 어떻게 방법이 달라지는지를 살펴보겠습니다.
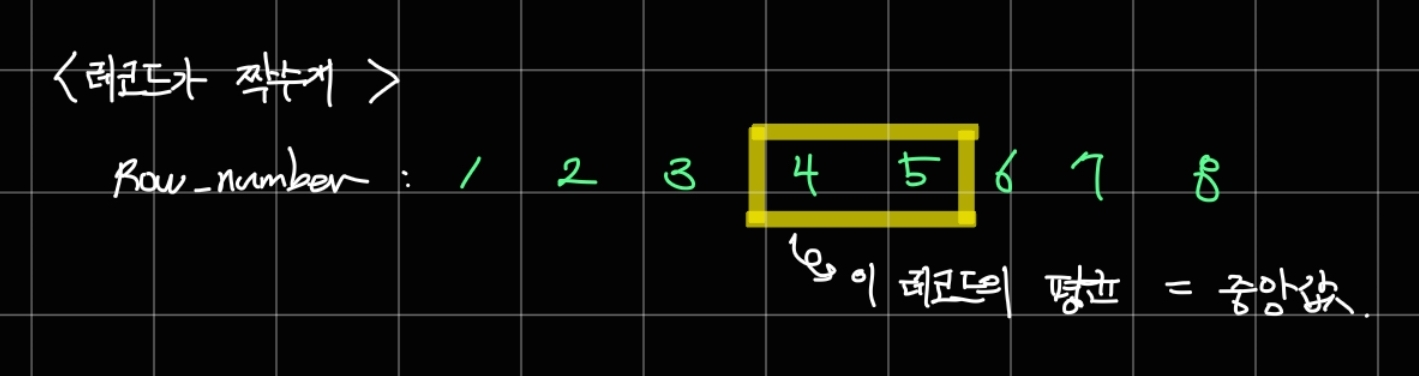
< 레코드가 짝수개일 때 >
레코드의 수가 짝수개일 땐 레코드의 정중앙값이 하나의 값으로 떨어지지 않습니다.
그렇기 때문에 정중앙의 앞/뒤에 위치한 레코드의 평균값을 중앙값으로 정의하는데요.
아래의 예시의 경우 4번째, 5번째 레코드의 평균값을 중앙값으로 취급합니다.
< 레코드의 수가 홀수개일 때 >
레코드의 수가 홀수개일 땐 레코드의 정중앙값이 하나의 값으로 떨어지기 때문에 이 값을 중앙값으로 취급합니다.

그럼 이러한 부분들을 고려하여 중앙값을 구하는 두 가지 방법에 대해서 알아보도록 하겠습니다.
이번 포스팅에서 사용하는 데이터는 아래와 같습니다.
select * from person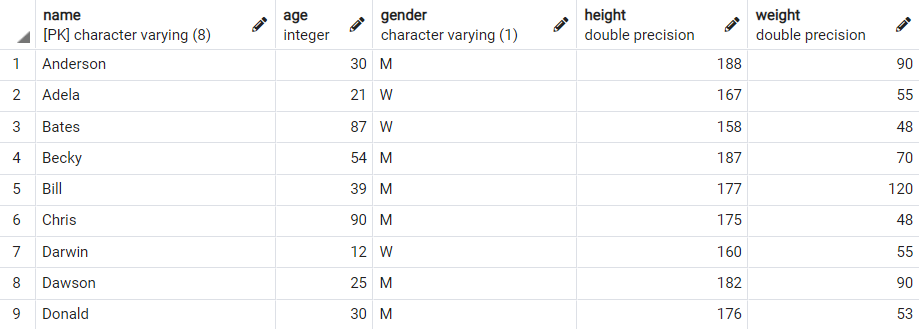
그럼 위 데이터를 이용하여 같은 성별(gender) 내, 키(height)의 중앙값을 구해보도록 하겠습니다.
(비추천) 방법 1 : row_number() 오름차순, 내림차순 이용
첫 번째 방법은 값을 오름차순으로 나열한 순서와 내림차순으로 나열한 순서를 비교하는 방식입니다.
쿼리 작성 프로세스를 생각해보면 아래와 같습니다.
< 방법 1의 흐름 >
1. 값을 오름차순으로 정렬한 컬럼(rownum_asc)을 만든다.
2. 값을 내림차순으로 정렬한 컬럼(rownum_desc)을 만든다.
3.1. (홀수) rownum_asc 와 rownum_desc 가 같은 값을 뽑아낸다.
3.2. (짝수) rownum_asc 와 rownum_desc 의 차이의 절대값이 1인 값들의 평균을 구한다.
이 방법을 활용한 쿼리는 아래와 같이 작성됩니다.
select gender, avg(height) median_height
from(
select gender, height
, row_number() over(partition by gender order by height asc) as rownum_asc
, row_number() over(partition by gender order by height desc) as rownum_desc
from person
) a
where abs(rownum_asc - rownum_desc) <= 1
group by 1;이 쿼리를 실행하면 아래와 같은 결과값을 얻을 수 있습니다.
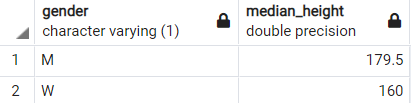
그런데 이 방식에는 몇 가지 문제점이 있습니다.
문제점 1.
row_number() 를 통해 오름차순, 내림차순을 구할 때, 동일한 값이 여러개 존재한다면 row_number()의 값이 동일값 내에서 순서가 무작위로 부여됨.
이러한 문제로 마지막 where 절에서 abs(rownum_asc - rownum_desc) 을 할 때, 중앙값이 제대로 추출되지 않는 문제가 발생함.
약간 말로 설명하기가 어려움이 있어 이해를 돕기 위해 예시를 들어보겠습니다.
< 이상적인 과정 >
우선 우리가 기대한 이상적인 과정을 나타내보면 아래와 같이 나타낼 수 있습니다.

오름차순, 내림차순으로 정렬한 값들의 차이의 절대값이 1 이하인 값을 가져오면 중앙값을 가져올 수 있습니다.
하지만 위에서 말한 동일한 값이 존재할 때에는 문제가 발생합니다.
< 문제 발생 case_짝수 >
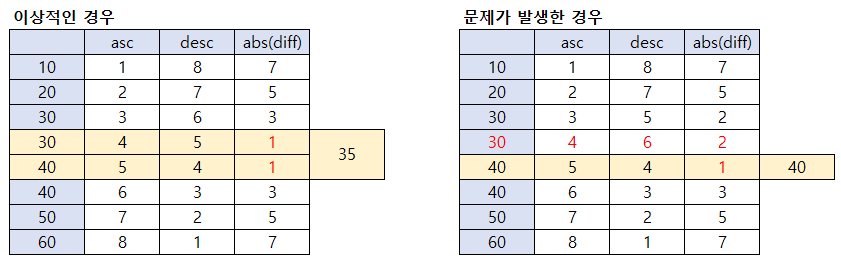
레코드의 수가 짝수일 때, 30 이라는 값에서 오름차순 및 내림차순의 인덱스가 기대했던 바와 다르게 형성된 경우입니다.
30의 인덱스가 (3,6), (4,5) 가 아닌 (3,5), (4,6) 이 되어 두 인덱스의 차이가 1이 되지 않는 문제가 발생했습니다.
이러한 이유로 중앙값은 35가 되어야하지만, 40으로 추출되는 문제가 발생합니다.
< 문제 발생 case_홀수 >

레코드의 수가 홀수일 때에는 중앙값을 구하는데에는 문제가 없지만 그 과정이 조금 애매합니다.
홀수일 땐 하나의 값이 추출되어 중앙값이 구해지는데, 2개의 값이 추출되어 평균값이 추출될 수 있기 때문입니다.
물론 값에는 차이가 없지만 우리가 생각했던 흐름에서 조금 엇나가있다는 느낌을 줍니다.
이러한 문제가 발생하기 때문에 이 방법으로 중앙값을 구하는 것은 무리가 있습니다.
또한 이 방법은 값을 잘못 추출할 뿐만 아니라 성능상의 문제도 발생합니다.
문제점 2
윈도우 함수인 row_number() 을 2번 사용하게 되면서 성능상의 비효율을 가져옴
윈도우 함수인 row_number()을 활용하게 되면 정렬(sorting)의 과정이 들어가야하기 때문에 성능의 저하가 발생합니다.
그런데 방법1의 경우 row_number() 함수를 2번 사용하게 되면서 성능상 비효율을 발생시킵니다.
이러한 2가지 문제점때문에 방법 1을 사용하기 보다는 다른 방법을 활용하는 것이 좋습니다.
🚩 방법 2 : (2*rownum - tot_cnt) between 0 and 2
위에서 살펴본 방법1의 문제점을 해결하기 위해 다른 방식으로 중앙값을 구할 필요가 있습니다.
두 번째 방법에서는 row_number()와 count() 함수를 사용하여 중앙값을 구합니다.
두 번째 방법의 과정을 따라가보면 아래와 같이 나타낼 수 있습니다.
< 방법2의 흐름 >
1. 값을 오름차순 or 내림차순으로 정렬한 컬럼(rownum)을 만든다.
2. 중앙값을 구하려는 값들의 전체 row 수 컬럼(tot_cnt)을 구한다.
3. rownum 값에 2를 곱해준 뒤 tot_cnt를 빼준다. (2*rownum - tot_cnt)
4. (2*rownum - tot_cnt) 의 값이 0 이상 2 이하인 값을 가져온다. ((2*rownum - tot_cnt) between 0 and 2)
위 과정을 쿼리를 작성하면 아래와 같이 작성할 수 있습니다.
select gender
, avg(height) as median_height
from(
select gender, height
, row_number() over(partition by gender order by height asc) as rownum
, count(1) over(partition by gender) as tot_cnt
from person
) a
where (2*rownum - tot_cnt) between 0 and 2
group by 1이 방법의 point 는 2*rownum - tot_cnt 의 부분입니다.
2*rownum 는 중앙값에 해당하는 rownum의 값과 tot_cnt 의 값의 수준을 비슷하게 만들어주기 위한 과정입니다.
그리고 두 값의 차이를 구해 값의 차이가 0 이상 2 이하에 속하는 값을 중앙값으로 뽑아오겠다는 의미이죠.
차이가 0 이상 2 이하인 값을 가져오는 이유는 레코드의 수가 짝수, 홀수인 경우를 모두 고려하기 위함입니다.
이 부분을 아래 그림과 함께 살펴보시면 이해가 쉬울것이라고 생각합니다.

이렇게 작성하여 얻은 결과값은 방법1과 같은 결과를 도출할 수 있었습니다.

이 방식은 방법1이 가지는 두가지 문제점을 보완할 수 있는 방법입니다.
동일한 값이 존재하더라도 값 계산에 문제가 발생하지 않고, 전체 테이블을 정렬하는 row_number() 함수를 1회만 사용했기 때문입니다.
그렇기 때문에 방법1을 사용하는 것 보다는 방법2를 사용하는 것을 추천합니다.
이렇게 끝내긴 아쉬우니 한가지 방법을 더 소개하고 포스팅을 마치려 합니다.
🚩 방법 3 : rownum between floor(tot_cnt) and ceil(tot_cnt)
마지막 방법도 마찬가지로 row_number() 와 count() 를 이용해서 중앙값을 구하는데요.
비슷한 방식이지만 이렇게도 구해볼 수 있다는 것을 보고 넘어가주시면 될 것 같습니다.
세 번째 방법의 과정을 따라가보면 아래와 같습니다.
< 세 번째 방법의 흐름 >
1. 값을 오름차순 or 내림차순으로 정렬한 컬럼(rownum)을 만든다.
2. 중앙값을 구하려는 값들의 전체 row 수 컬럼(tot_cnt)을 구한다.
3. (tot_cnt + 1)/2 의 값을 구해준다.
4. rownum이 floor((tot_cnt + 1)/2) 와 ceil((tot_cnt + 1)/2) 사이에 존재하는 값을 추출한다.
(rownum between floor((tot_cnt+1)/2) and ceil((tot_cnt+1)/2))
위 과정을 쿼리로 작성하면 아래와 같습니다.
select gender
, avg(height) as median_height
from(
select gender, height
, row_number() over(partition by gender order by height asc) as rownum
, cast(count(1) over(partition by gender) as numeric) as tot_cnt
from person
) a
where rownum between floor((tot_cnt+1)/2) and ceil((tot_cnt+1)/2)
group by 1이 방식의 point 는 (tot_cnt+1)/2 를 해주는 부분입니다.
우선 이 방식을 떠올리게 된 과정을 따라가보면 이해가 쉬울 것 같습니다.
1. '방법2' 에서 rownum * 2 를 해줬으면 비슷한 논리로 tot_cnt/2 를 해줘도 될 것 같은데?
2. 그럼 rownum 와 tot_cnt/2 의 값을 비교해서 중앙값을 구해보자
3. tot_cnt/2 의 값을 올림한 값(ceil)과 내림한 값(floor) 사이에 rownum 이 들어가면 되겠네!
4. 그런데 tot_cnt/2 를 했을 때, tot_cnt 가 짝수인 경우엔 ceil, floor 값이 같고 홀수인 경우엔 ceil, floor 값이 다른 문제가 생기네
5. 그러면 (tot_cnt+1)/2 을 해서 문제를 해결하고 중앙값을 구해야겠다.
이러한 과정의 결과로 세 번째 방법을 생각할 수 있었는데요.
마찬가지로 이해를 돕기 위해 이 과정을 그림으로 살펴보면 아래와 같습니다.
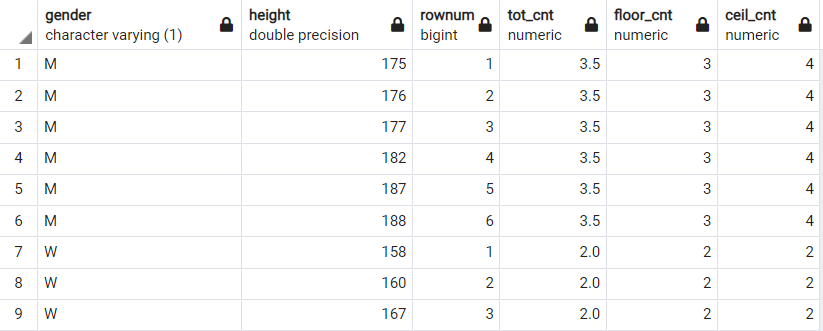
이렇게 만들어낸 floor() 값과 ceil() 값 사이에 rownum 이 들어가는 값을 추출하여 중앙값을 구할 수 있습니다.
3. 끝마치며
이렇게 이번에는 중앙값읠 median 함수 없이 구해보는 시간을 가져봤습니다!
엑셀에서도 median 함수를 통해 쉽게 구할 수 있는 중앙값이지만 SQL 에서는 조금 번거로운 부분이 있네요.
아마도 SQL이 행과 행간의 관계를 다루는데 어려움이 있는 구조라 그런 것 같습니다.
그래도 이렇게 함수들을 직접 구현해보는 재미도 있으니 재미있게 읽어주셨길 바랍니다 :)
'#1 언어 노트 > #1.1. SQL 노트' 카테고리의 다른 글
| [SQL] with 절을 효율적으로 사용하기 (4) | 2022.10.02 |
|---|---|
| [SQL] Index 를 이용해서 효율적인 쿼리 작성하기 (2) | 2022.08.21 |
| [SQL] SQL에서 정규표현식 활용하기 (5) | 2022.06.10 |
| [SQL] 윈도우 함수(Window Function)의 소중함을 느껴보자 (6) | 2021.12.19 |
| [SQL] 성능 관점에서의 서브쿼리(Subquery) (13) | 2021.09.26 |
블로그의 정보
고동의 데이터 분석
소라고동_