[개념] 통계적 가설 검정의 과정 훑어보기
by 소라고동_0. 들어가며
데이터를 통해 어떠한 의사결정을 할 때에는 가설을 설정하고 이를 검정하는 과정을 거치게 되는데요.
가설을 설계하고 테스트를 진행한 후 결과가 나온다면 우리는 '이 실험의 결과를 믿을 수 있을까?' 라는 고민을 하게 됩니다.
그래서 이번 포스팅에서는 판단의 과정에서 필요한 개념인 통계적 가설 검정에 대하여 다뤄보려 합니다.
(이번 포스팅에서는 값을 계산하거나 수식을 도출하는 내용을 담지 않았습니다. 그저 가설 검정의 과정을 흐름에 따라 살펴보는 목적입니다.)
1. 통계적 가설 검정이란?
먼저 통계적 가설 검정이라는 단어를 하나하나 뜯어보겠습니다.
가설
어떤 사실을 설명하거나 어떤 이론 체계를 연역하기 위하여 설정한 가정.
(출처 : 네이버 어학사전)
가설이라는 것을 쉽게 이야기하면 우리가 궁금해하는 내용을 정의해보는 단계라고 생각을 할 수 있습니다.
예를 들어, 마케팅 채널 A 와 B를 운영할 때 마케팅 채널 B 에서 유입된 유저가 발생시키는 매출액이 더 높지 않을까? 라는 궁금즘을 바탕으로 아래와 같은 가설을 정의할 수 있습니다.
마케팅 채널 A 보다 마케팅 채널 B 에서 유입된 유저가 발생시키는 매출액이 더 높을 것이다.
이렇게 정의한 가설이 옳은지 판단하기 위해서 검정의 과정을 거치게 되는데요.
검정
일정한 규정에 따라 자격이나 조건을 검사하여 결정함.
(출처 : 네이버 어학사전)
우리가 정의한 가설이 어떠한 조건을 만족하는지를 살펴보고 그 '가설이 옳다/그렇지 않다'를 검정하게 됩니다.
그런데 우리는 이렇게 가설 검정을 진행할 때 실험의 대상을 샘플링하게 됩니다.
즉, 모든 유저를 대상으로 확인하지 않고 몇몇 유저를 샘플링하여 실험을 진행한다는 것이죠.
아래의 그림을 보시면 모집단과 표본집단의 개념을 쉽게 이해할 수 있습니다.

이렇게 모집단 전체를 대상으로 하지않고 표본을 뽑아 실험하고 가설을 검정하는 이유가 있는데요.
1. 전체를 대상으로 실험을 한다면 너무 많은 시간이 소요되어 결과를 서비스에 반영하는데 비효율을 가져온다.
2. 마찬가지로 많은 비용이 사용되기 때문에 비효율적이다.
이렇게 시간적, 비용적인 효율을 위해서 표본을 선정하고 이에 대한 분석을 진행하게 됩니다.
여기서의 핵심은 '표본에 대한 실험의 결과가 전체를 대표할 수 있을까?' 라는 부분이 되는데요.
이 부분을 확인하기 위해 통계적인 방법을 활용하게 됩니다.
이렇게 우리는 실험에 대한 결과를 파악하기 위해 통계적 가설 검정의 과정을 진행하게 됩니다.
그런데 통계학에서 가설의 검정하는 방식은 우리가 기대하는 것과는 조금의 차이가 있습니다.
기대하는 바 : 마케팅 채널 A 보다 마케팅 채널 B 에서 유입된 유저가 발생시키는 매출액이 더 높을 것이다.
통계학에서의 검정 결과 : 마케팅 채널 A와 마케팅 채널 B에서 유입된 유저가 발생시키는 매출액은 차이가 있다고 판단할 수 있다.
두 그룹에 대한 매출액의 비교 결과를 알려주는 것이 아니라, 두 그룹의 차이가 있다는 것이 통계적으로 유의하다라는 것만을 알려주는 것이죠.
이러한 과정에서 우리가 알아야 하는 개념들을 흐름에 따라 몇 가지 살펴보겠습니다.
2. 알아둘 개념
2.1. 귀무가설과 대립가설
먼저 통계적 가설 검정을 위해 귀무 가설과 대립 가설을 정의합니다.
귀무가설(Null Hypothesis, H0)
: 의미있는 차이가 없는 경우의 가설으로 이것이 맞거나 맞지 않다는 통계학적 증거를 통해 증명하려는 가설
( = 우리가 기각하려는 가설, 기본적으로 옳다고 가정하는 가설)
대립가설(Alternative Hypothesis, H1)
: 귀무가설과 반대되는 가설
(= 우리가 입증되기를 기대하는 예상이나 주장하는 가설)
귀무가설 (H0) 마케팅 채널 A 와 마케팅 채널 B 에서 유입된 유저가 발생시키는 매출액은 같을 것이다. 대립가설 (H1) 마케팅 채널 A 보다 마케팅 채널 B 에서 유입된 유저가 발생시키는 매출액이 더 클 것이다.
우리는 가설 검정을 통해 귀무가설을 기각시키고 대립가설이 채택하기를 기대하게 됩니다.
2.2. 표본 평균과 모평균, 중심 극한의 정리
표본 평균 : 모집단 내의 표본 집단에 대한 평균
모평균 : 모집단 전체에 대한 평균
우리는 표본 집단을 통해 모집단을 추정하게 되는데요.
표본 집단의 평균(표본 평균)이 모집단의 평균(모평균)을 대표하는지를 살펴봐야 한다고 이야기했습니다.
표본집단을 통해 모집단을 추정할 때 사용되는 아주 중요한 개념이 있는데요.
바로 중심 극한의 정리입니다.
중심 극한의 정리 (Central Limit Theorem)
: 표본 집단의 수가 충분이 클 때, 모집단의 분포와 관계없이 통계학적으로 표본집단의 평균은 정규분포를 따른다
아래의 그림을 살펴보면 이해가 조금 더 편할 것 같습니다.

각각의 표본 집단들의 평균을 하나의 분포도로 나타내어보면 정규분포를 따른다는 것입니다.
이렇게 표본들의 평균이 정규분포를 따른다는 것이 우리에게 주는 의미는 생각보다 큽니다.
앞서 이야기했듯, 모집단 전체를 실험할 수 없는 상황때문에 우리는 늘 표본집단을 기반으로 실험을 진행하고 실험의 성과를 판단하게 됩니다.
그런데 이렇게 표본의 평균이 정규분포를 따른다는 의미는, 특정한 사건이 일어날 확률을 계산할 수 있다는 이야기입니다.
우리는 평균들의 집단이 정규분포를 따른다고 하니 검정통계량(t-통계량, F-통계량 등)을 활용하여 특정 사건이 발생할 확률을 알게 되고, 이를 통해 가설 검정을 진행할 수 있게 됩니다.
그러면 중심극한의 정리를 활용하여 표본평균들의 분포을 통해서 모집단의 평균을 추정할 수 있다는 것을 알게 되었는데요.
그러면 어떤 과정을 통해 모평균을 추정할 수 있는걸까요?
그 개념을 알기 위해서 신뢰 구간과 구간 추정에 대한 이야기를 할 필요가 있습니다.
2.3. 신뢰 구간과 구간 추정
우리는 실제로 모평균의 분포가 어떠한지 모르니, 우리는 충분히 큰 표본집단의 분포(=정규분포)를 통해 검정을 진행하게 됩니다.
그런데 하나의 표본집단에 대한 평균 값을 구해놓고 이 값이 모집단을 대표할것이라고 판단하기엔 뭔가 찜찜합니다.
왜냐하면 표본을 뽑아봤을 때 하필 이 표본들의 매출액이 유독 높아서 표본집단의 평균값이 아주 높게 나올 수 있기 때문입니다.
그래서 우리는 여러 표본들의 평균을 구해놓고, 표본평균과 표본 표준편차를 활용하여 '이 정도 구간 안에는 모집단의 평균이 속하지 않을까?' 라는 생각을 하게 됩니다.
이 구간을 신뢰 구간이라고 하고, 이 신뢰구간을 이용해서 모평균을 추정하게 됩니다.
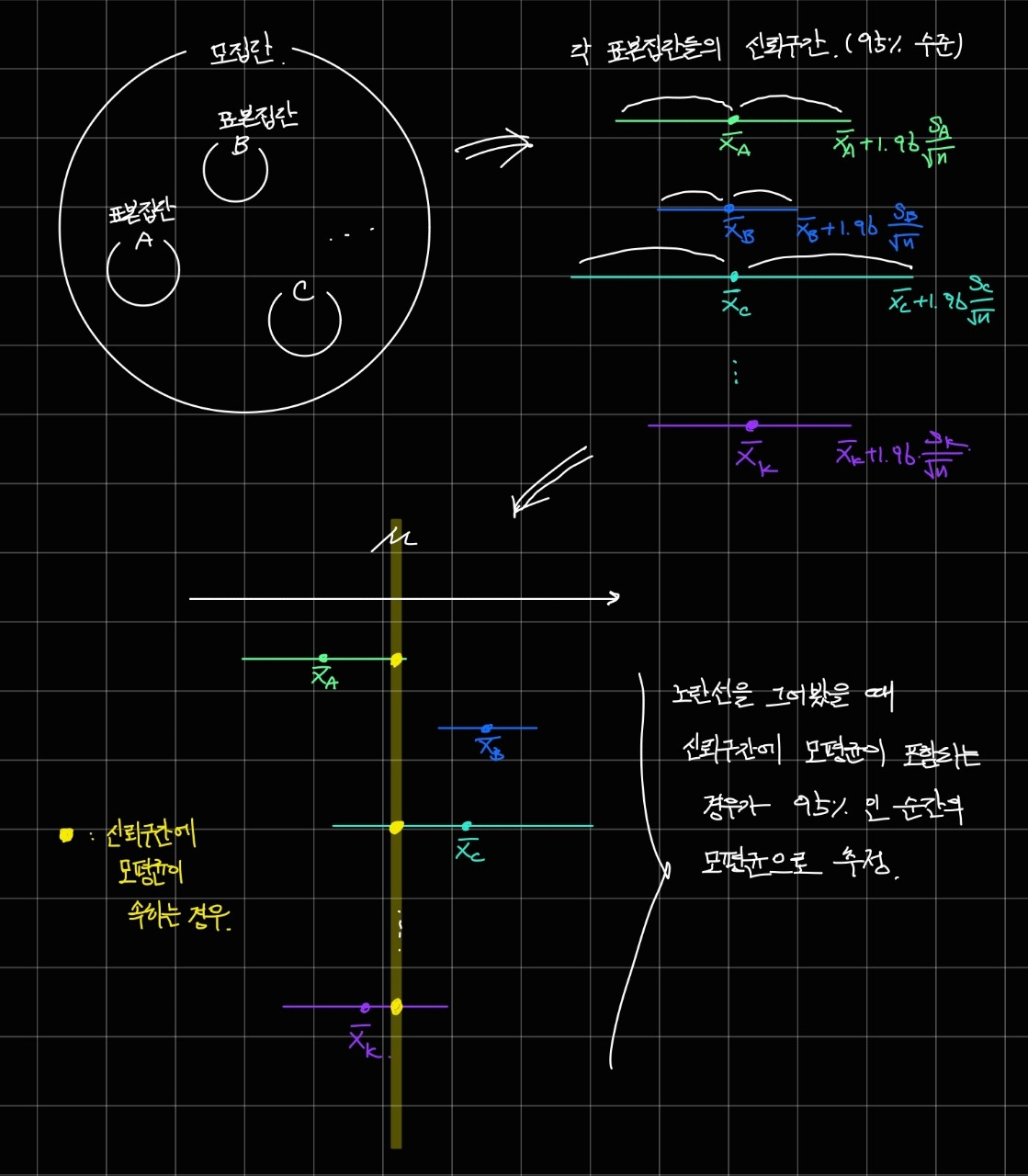
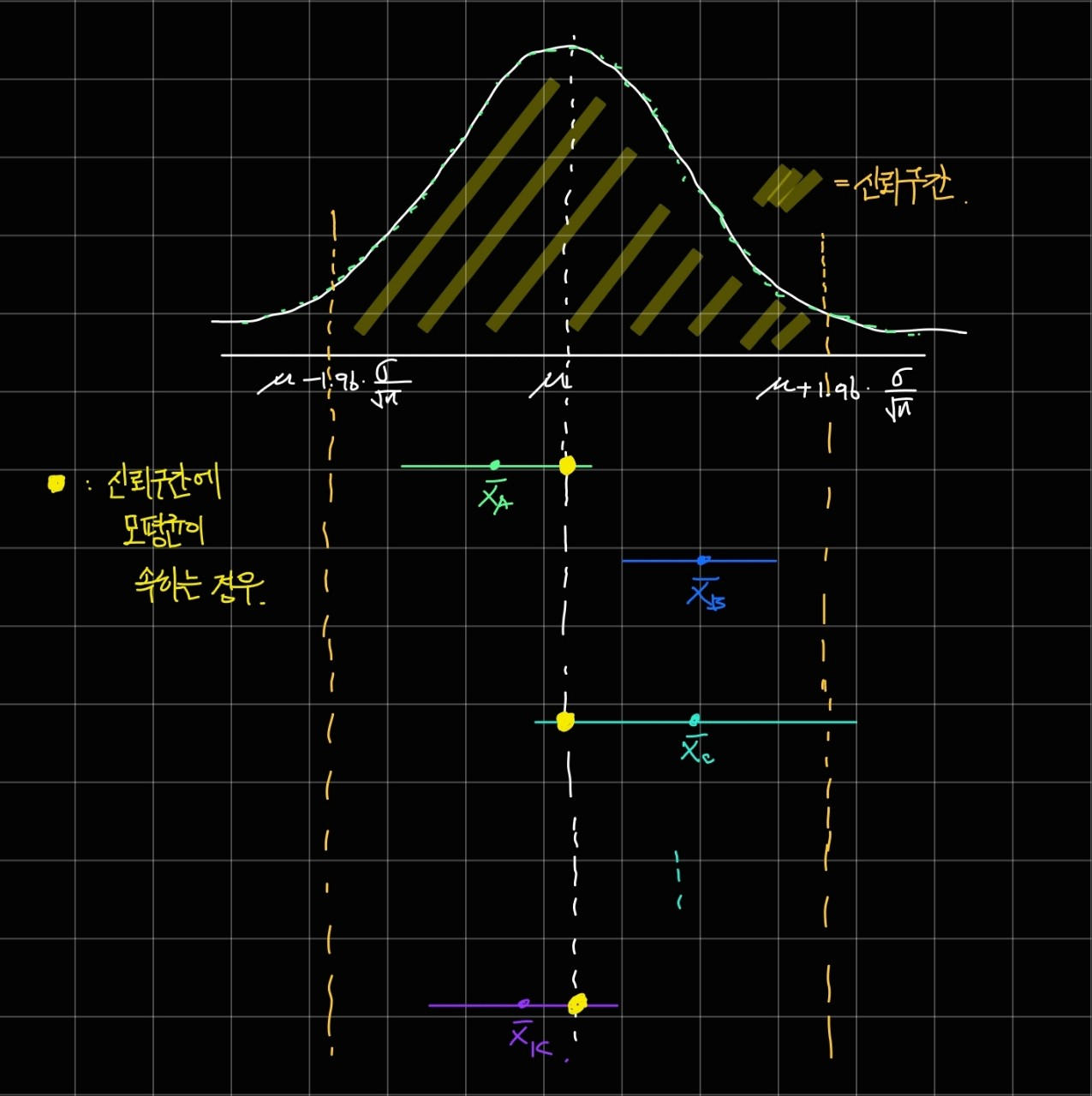
왼쪽 그림은 95% 수준의 신뢰구간을 통해 모평균을 추정하는 과정을 담고 있고, 오른쪽 그림은 추정된 모평균으로부터 만들어진 신뢰구간을 나타내고 있습니다.
그리고 우리가 신뢰 수준을 어느 정도 수준으로 정하느냐에 따라서 신뢰 구간이 넓어지고 좁아질 수 있습니다.
(이번 포스팅에서는 표본의 수가 동일한 것으로 가정했습니다.)
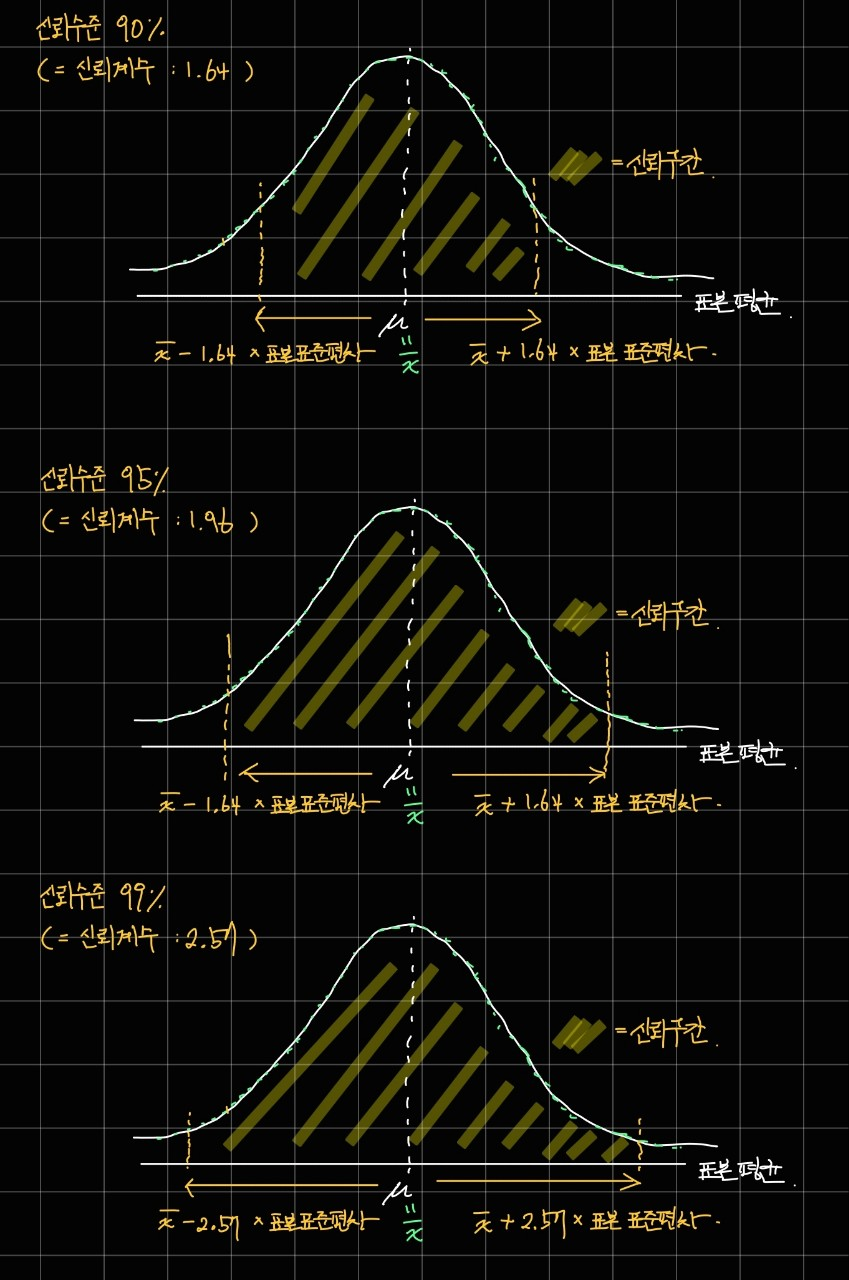
신뢰 수준이 높아질수록 신뢰 구간이 넓어지는 모습을 확인할 수 있습니다.
이는 신뢰 수준이 높을수록 모평균이 우리가 추정한 표본 평균의 구간 안에 들어있을 확률이 높아진다는 것이고,
오차가 생길 가능성은 낮아지지만, 추정의 가치도 낮다라는 의미를 내포하고 있습니다.
그럼 우리가 설정했던 귀무가설을 기각할지 채택할지는 어떻게 판단을 할까요?
우선 두 채널의 표본 분포가 아래와 같이 겹치지 않을 경우라면 판단이 어렵지 않습니다.
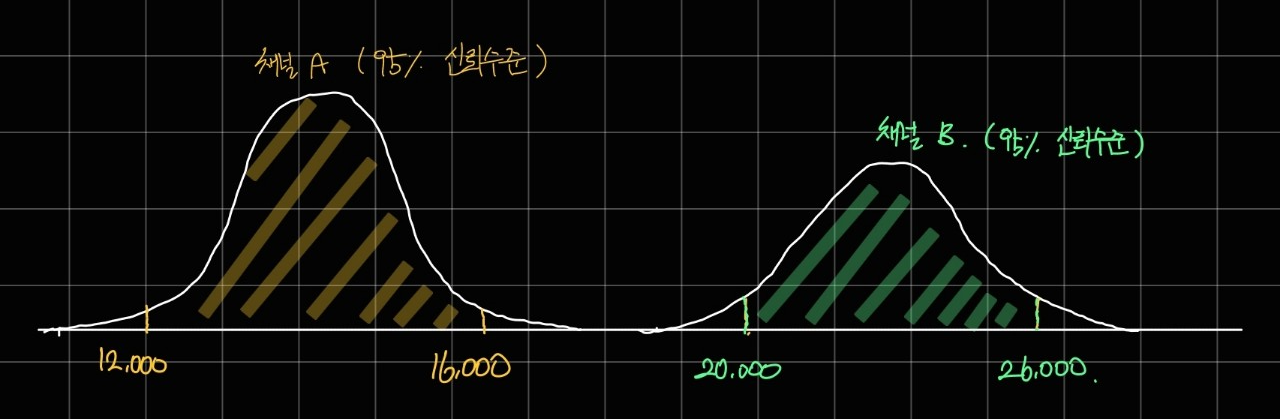
이 경우는 두 채널의 신뢰구간이 겹치지 않기 때문에 귀무가설을 기각할 수 있습니다.
(= 마케팅 채널 A 보다 마케팅 채널 B 에서 유입된 유저가 발생시키는 매출액이 더 클 것이다.)
왜냐하면 두 채널이 95%의 신뢰 수준에서 신뢰 구간을 가지는데, 그 범위가 겹치지 않으니 두 채널의 표본 평균이 유의하게 다르다고 해석할 수 있기 때문입니다.
그런데 만약 아래와 같이 두 분포가 겹치는 경우라면 어떨까요?
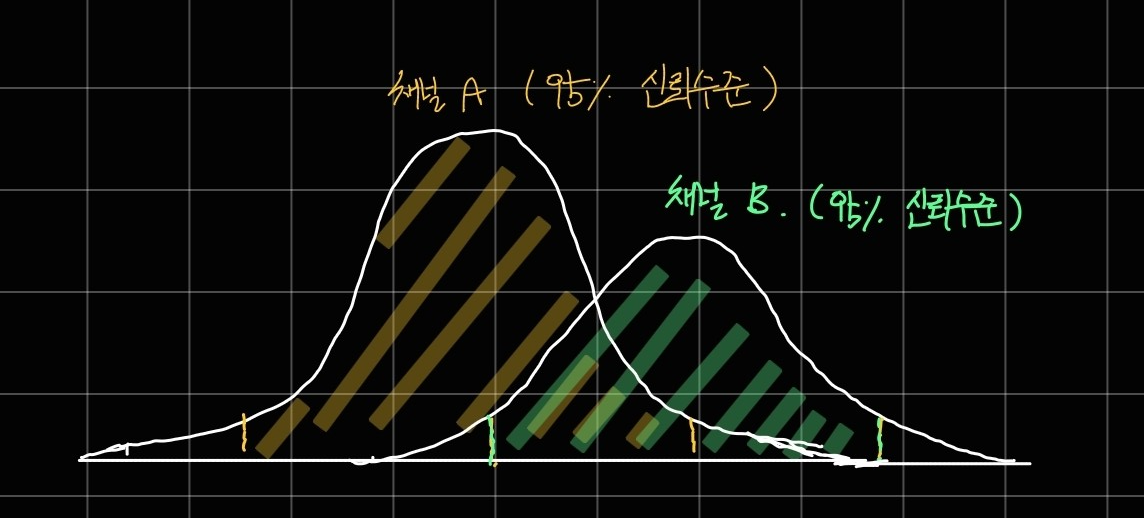
이러한 경우에는 검정통계량과 사전에 정의한 오류 수준을 이용해서 구한 p-value를 통해 두 분포가 유의하게 차이가 있는지를 판단하게 됩니다.
2.4. 오류 수준 (1종 오류, 2종 오류), p-value
이렇게 두 분포가 겹쳐있을 때 통계적으로 두 분포의 차이가 유의한지의 여부를 결정하게 되는데요.
여기서 또 하나의 문제는 실험을 통해 귀무가설의 기각 여부를 판단할 때 오류가 발생할 가능성이 있다는 것입니다.
실험 결과는 결국 표본으로부터 얻은 데이터이기 때문에 항상 오류가 발생할 가능성이 존재한다는 것이죠.
오류의 종류는 크게 1종 오류와 2종오류로 나뉩니다.
제 1종 오류 : 귀무가설이 참인데 기각한 경우
제 2종 오류 : 귀무가설이 거짓인데 채택한 경우
많이 보셨을 표를 통해 나타내면 아래와 같습니다.
| 귀무가설 참 | 귀무가설 거짓 | |
| 귀무가설 채택 | 옳음 (1-α) | 제 2종 오류 (β) |
| 귀무가설 기각 | 제 1종 오류 (α) | 옳음 (1-β) |
이를 예시를 통해 살펴보겠습니다.
| 오류 | 내용 |
| 제 1종 오류 | 마케팅 채널 A 와 B 에서 유입된 유저의 매출액 차이가 없는데, 있다고 판단한 경우 |
| 제 2종 오류 | 마케팅 채널 A 보다 B 에서 유입된 유저의 매출액이 더 큰데, 그렇지 않다고 판단한 경우 |
그렇다면 제 1종 오류와 제 2종 오류 중 어떤 오류가 더 위험할까요?
경우에 따라 다르겠지만 보통은 제 1종 오류를 더 위험하게 여긴다고 합니다.
왜냐하면 과학적으로 어떠한 실험을 할 때, 실제로 증거가 없는데 있다고 오해해서 생기는 위험성을 더 경계하기 때문입니다.
일반적으로 제 1종 오류에 대한 기준은 5%인데, 이는 신뢰 수준이 95% 수준이라는 의미와 동일합니다.
(실험을 진행하기 전에 제 1종 오류(차이가 없는데 있다고 판단하는 오류)의 수준을 미리 정해둡니다.)
만약 실험의 결과가 아래와 같이 나타났다고 가정해봅시다.
| 마케팅 채널 | 유저 1인당 평균 매출액 | 매출액 차이 (B-A) |
| 채널 A | 17,000 원 | 3,000 원 |
| 채널 B | 20,000 원 |
이 기준에 따라서 가설 검정을 진행해보면 아래와 같이 나타낼 수 있습니다.
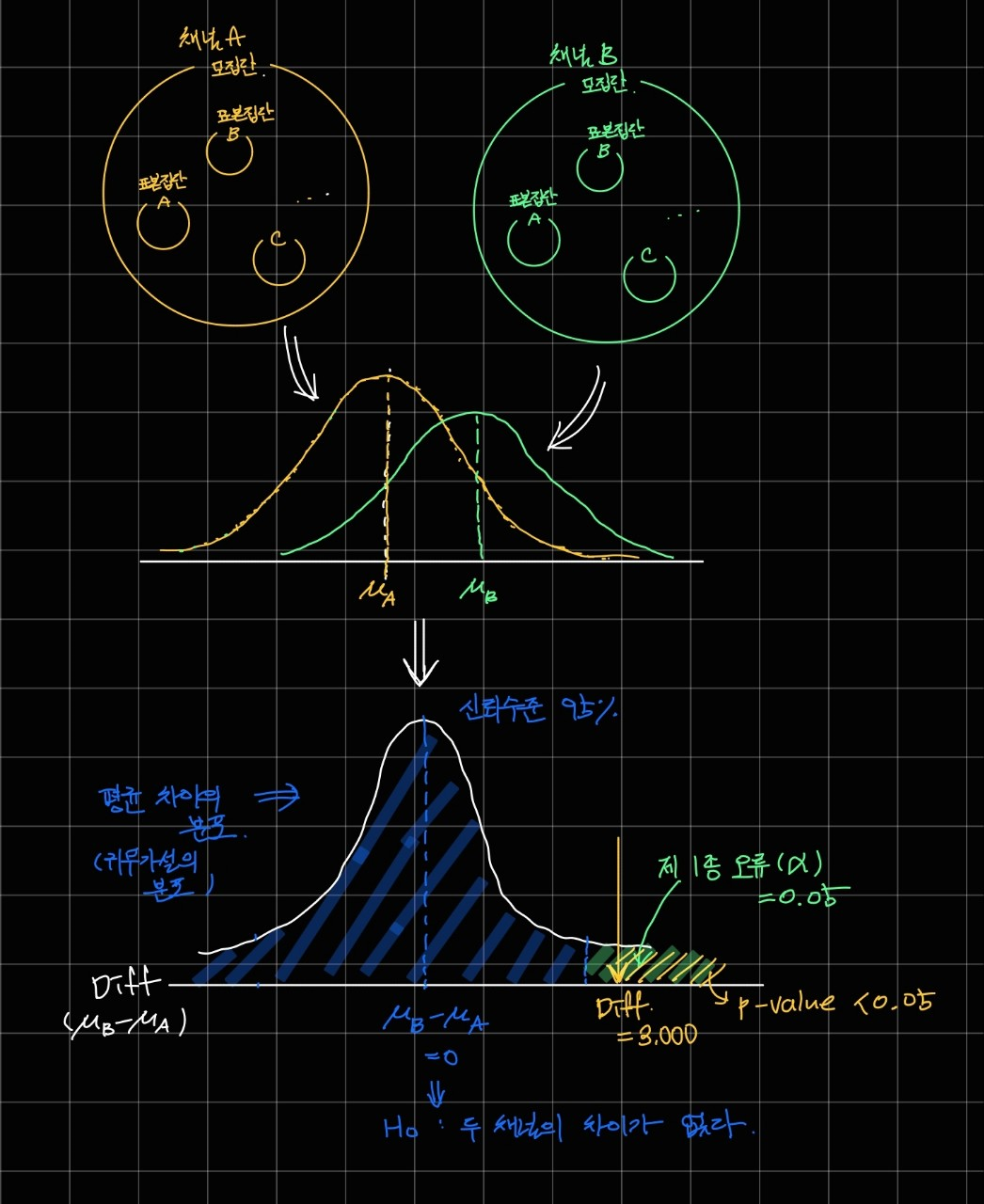
두 채널의 평균의 차이를 나타내는 분포도를 그려 이를 통해 가설을 검정하게 되는데요.
위 예시를 살펴보면 귀무가설이 옳다는 가정 하에서 '채널 B 의 유입 고객의 매출액이 채널 A 보다 크지 않은데, 크다고 할 오류 수준(=0.05)' 보다 p-value가 낮습니다.
이는 우리가 실험으로부터 얻은 매출액의 차이 값이 유의수준에 해당하는 임계값보다 분포도 상 오른쪽에 있다는 것으로 알 수 있습니다.
여기서 p-value는 이런 의미를 담고 있습니다.
p-value
: 귀무가설이 옳다는 전제 하에서 관찰된 검정통계량만큼의 극단적인 값이 관찰될 확률
그리고 '채널 B 의 유입 고객의 매출액이 채널 A 보다 크지 않은데, 크다고 할 오류 수준(=0.05)'보다 p-value가 낮습니다. 라는 문장을 쉽게 풀어서 이야기를 해보면 이렇습니다.
귀무가설이 옳다고 했을 때, 100번의 표본 추출 중 95번은 두 채널의 차이가 신뢰구간 안에 들어가는게 맞지.
그런데 그 구간 안에 들어가지 않았다고?
→ 이렇게 극단적으로 값이 관찰될 확률이 아무리 커도 5%보다 작을텐데.. (p-value < 0.05)
→ 그럼 A 채널보다 B 채널에서 유입된 유저의 매출액이 더 큰거구나?
→ 그렇다면 귀무 가설이 잘못되었다는 이야기니깐 기각해야겠다.
이러한 흐름에 따라서 귀무가설을 기각하고 대립가설을 채택하게 됩니다.
이렇게 귀무가설을 기각하고 대립가설을 채택하게 되면 우리의 실험 결과가 유의하구나! 라고 판단할 수 있게 됩니다.
3. 끝마치며
이렇게 통계적 가설 검정을 통해서 귀무가설을 기각하고 대립가설이 통계적으로 유의하다는 것을 알 수 있습니다.
하지만 우리의 목적은 '그래서 이 결과가 비즈니스적으로 얼마나 이득이 되는데?' 라는 질문의 답을 찾는 것입니다.
그러니 이렇게 실험의 결과가 '마케팅 채널 B에서 유입된 유저가 발생시키는 매출액이 3.000원이나 높으니 이 채널이 더 좋아' 라고 판단하기 전에 다양한 지표들과 함께 판단을 해야합니다.
예를 들어 채널 B 의 매출액이 3,000이 더 높았지만 고객 획득 비용이 3,500원 더 높았다면, 마케팅 채널 B의 효율이 더 낮다는 결론을 내릴 수 있는 것 처럼 말이죠.
이번 포스팅에서 다룬 내용은 해당 개념들의 겉만 훑고지나간 느낌이기 때문에 궁금증이 생기는 부분이 있다면 조금 더 심도깊게 공부할 필요도 있어보입니다.
대학생때부터 접했지만 아직까지도 헷갈리는 개념들에 대해 정리를 해보았고, 또 기억이 나지 않을 때마다 이 포스팅을 보며 기억을 살려봐야겠습니다.
잘못된 부분이 있다면 댓글을 통해 알려주시면 감사하겠습니다!
'#2 분석 노트 > #2.1. 분석 방법 및 개념' 카테고리의 다른 글
| [분석] 공급사 분석 리포트 작업 회고하기 (4) | 2023.04.09 |
|---|---|
| [분석] 지표를 제대로 바라보려면? (0) | 2023.02.24 |
| [개념노트] AARRR을 책으로 배웠습니다 #4: 수익화(Revenue) (0) | 2022.01.31 |
| [개념] 실생활에서 바라본 고객 생애 가치(LTV) (0) | 2022.01.19 |
| [실습] SQL을 활용한 리텐션 분석하기 (2) | 2021.10.21 |
블로그의 정보
고동의 데이터 분석
소라고동_